こんにちは!管理人のアカツキです。
最近、災害についてより詳しく知りたい!との思いから関連する書籍を購入して読んでいます。
そして読み終わったのならば、その書籍はどのような本であったかを共有したいと考え、書評(とはいってもそこまでかしこまったものではありません)を始めています。
今回は「津波と波浪の物理」をご紹介します。
講談社「謎解き・津波と波浪の物理」
- 書籍名 謎解き・津波と波浪の物理 波長と水深のふしぎな関係
- 著者 保坂 直紀(ほさか・なおき)
- 定価 946円(税込み)
- 出版社 講談社
- シリーズ ブルーバックス
- ISBNコード 978-4-06-257924-7
- 発売日 2015年(平成23年)7月27日
講談社による自然科学系新書「ブルーバックス」シリーズからの一冊です。
前回は「富士山噴火と南海トラフ」という、同じくブルーバックスの一冊を取り上げました。
津波については前から少し勉強してみたいと思っており、ブルーバックスならそのような本もあるだろうと調べたところ、本書に巡り合いました。
著者はサイエンスライターをされている保坂直紀さんです。大学で海洋物理学を専攻されており、前著に「謎解き・海洋と大気の物理」などがあります。
それではその内容を見ていきましょう。まずは目次からです。
【目次】
まえがき
第1章 波、それは風の便りー波の誕生
1-1 はじまりはさざ波から
1-2 「波浪」と「津波」
1-3 どう生まれ、どう育つか
1-4 「波の科学」の基本的な考え方
第2章 波とはなにかー複雑な現象をシンプルに理解する
2-1 「波」の基本を押さえる
2-2 「水面の波」はなぜ伝わるか
2-3 複雑な海の波をどう攻略するか
第3章 風が起こす波ー風波のふしぎな世界
3-1 「水の動き」を分解する
3-2 波と水深の「深い関係」ーそこに「底」はあるか?
3-3 速い波、遅い波ーそして波は止まれない
3-4 「波の群れ」には謎がいっぱい
3-5 波の最期ー砕けて終えるその生涯
3-6 静かな海にも大きな波が!
第4章 津波の物理学ー「海底を感じる」長波のふしぎ
4-1 三陸を襲った巨大津波の謎
4-2 津波を科学する考え方
4-3 「海底を強く感じる波」ならではの現象
4-4 津波はなぜ「水の壁」へと変貌するのか
4-5 「海底を感じる波」の奇妙なふるまい
あとがき
本書は4章から構成されています。
まず波というものはどういうものかを1章で解説されています。
続く2章では波を理解するための用語などについての解説と海の波の複雑さについて、またそれをどう考えていくかの指針が描かれています。
3章からは波の現象の解説です。波の下にある水の動き方や、津波を理解するのに重要な用語となる長波といった波の種類などについて述べられています。
そして最終章の4章では、津波について丸々解説が行われています。
数式はありません
本書が大変面白いと感じたのは、この分野の本では必ずと言っていいほどある数式をほぼ全く使うことなく波(波動、はどうとも言いますね)という物理現象を説明していることです。
数式を使わず説明するということは、その現象をしっかりと理解していないとできないことだと思います。著者は丁寧にわかりやすく解説をされていると感じました。
ですので、数式を見ると思わず目を背けたくなる方も安心されても良いのではないでしょうか。
数式はもちろん大事ですが、大事なのはその物理現象の本質を理解することだと思いますから。
ただこれにはもう一つ理由がありまして、著者はまえがきでその理由を述べておられます。
その理由とは、波の現象を記述する数式がかなり難しい、ということにあります。
たとえば、津波の運動を表す方程式は次のような式で表されます。
(連続の式と非線形長波理論式)
$$\frac{\partial \eta}{\partial t}+\frac{\partial M}{\partial x}+\frac{\partial N}{\partial y}=0$$
$$\frac{\partial M}{\partial t}+\frac{\partial}{\partial x}\left(\frac{M^2}{D} \right) +\frac{\partial}{\partial y}\left(\frac{MN}{D}\right)+gD\frac{\partial \eta}{\partial x}+\frac{f}{D^2}MQ=0$$
$$\frac{\partial N}{\partial t}+\frac{\partial}{\partial x}\left(\frac{MN}{D} \right) +\frac{\partial}{\partial y}\left(\frac{N^2}{D}\right)+gD\frac{\partial \eta}{\partial y}+\frac{f}{D^2}NQ=0$$
\(\quad\eta\,\colon\,\)海面の上下変動、\(h\,\colon\,\)静水深、\(D=h+\eta\)
\(\quad g\,\colon\,\)重力加速度、\(f\,\colon\,\)摩擦係数、\(M,N\,\colon\,x,y\,\)方向の流量フラックス
\(\quad Q=\sqrt{M^2+N^2}\)
出展:「津波予報へのシミュレーション技術の活用」林 豊(気象研究所) 日本気象学会「第41回夏季大学 気象のシミュレーションII」
これは非線形長波(ちょうは)理論による方程式というものなのだそうです。
一般に偏微分(へんびぶん)方程式と言われるもので大学で学ぶレベルになります。
海岸近く以外(津波の発生場所から沖合まで)ではより式が簡略化されますが、それでも偏微分方程式であることには変わりなく取り扱いは難しいです。難しいですが、それを解く工夫がたくさんあります。
これらに適切な条件を与えてパソコンによる数値計算を行うことで、津波の高さや動きをシミュレーションすることが可能であり、実際に津波予報に活用されているとのことです。
少し横道に反れてしまいましたが、海の波というものはそれだけ物理的に取り扱うのが難しいということになります。そのようなこともあり、本書とは別に特設サイトも用意されています。
こちらでは本の中で述べられたいくつかの波について、動画が見られます。
しかも、実際に数式を解いて作られたものになっています。
ぜひこちらも参考にしてイメージを浮かべつつ、本書を読み進めてみてください。
3.11の津波は2つの波が重なっていた?
ここでは最終第4章について少し取り上げてみたいと思います。
この章ではすべて津波について述べられています。
津波はすでにどのようなものなのか、知識をお持ちの方も多いと思います。
本書においても、もちろん津波とは何か?といった所を解説しています。
ただいきなり津波とは?と述べるのではなく、実例を示してから説明をするというスタイルになっています。
その実例として取り上げられているのが、東日本大震災を起こした東北地方太平洋沖地震です。
私も本書を読んで初めて知ったのですが、実はあの時の津波は2つの波が重なったものだというのです。
その結果、岩手県宮古市では最大40.4mもの高さまで津波が這い上がってきたということです。
ちなみにこれを「遡上高(そじょうこう)」と言います。よく津波の高さと言いますが、これに関係する言葉にはいくつか種類があります。
本書ではこれらについても図を用いて分かりやすく示してくれていますよ。
海底を「感じる」波がある?
中盤では、津波がどのような波なのかについて物理的な解説がされています。
第3章までに述べられた波の基本がここでふんだんに使われていますので、もし分かりにくいところがある場合は前の章を読み返すということが必要になるかも知れません。
そして重要なことは、津波は「長波(ちょうは)」と呼ばれる波であるということです。
波には山と谷があり、その形を繰り返しています。
最初の山と次の山までの距離を波の長さ、波長(はちょう)と言います。
長波は、この波長が水深に比べてはるかに長い波のことを言います。
太平洋沖は一番深い日本海溝で8,000mほどですが、津波の波長は実に数百kmとも言われます。
1kmは1,000mですから、水深をざっくり10,000mとしても波長がそれよりも数十倍は長い、ということになります。
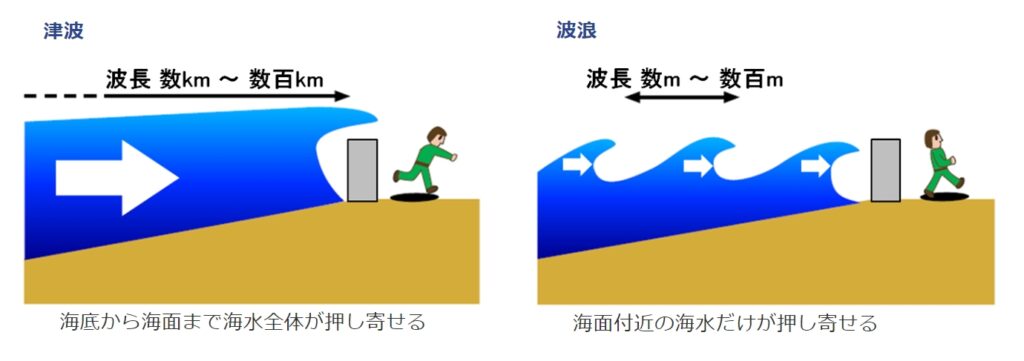
出展:気象庁「津波について」
このタイプの波は、水が海底から海面までまとめて同じスピードで動きます。
だからこそ、津波は普通の波と違って盛り上がった海面が絶え間なく押し寄せ、そして一気に引いていくのです。
本書ではこのような波を「海底が感じる波」と呼んでいます。
津波のおそろしさ
よく津波についてのおそろしさを述べたものに「津波のスピードはジェット機なみ」といったことがあります。実はこれも長波の性質によるものです。長波が進む速度は、重力と水深で決まります。
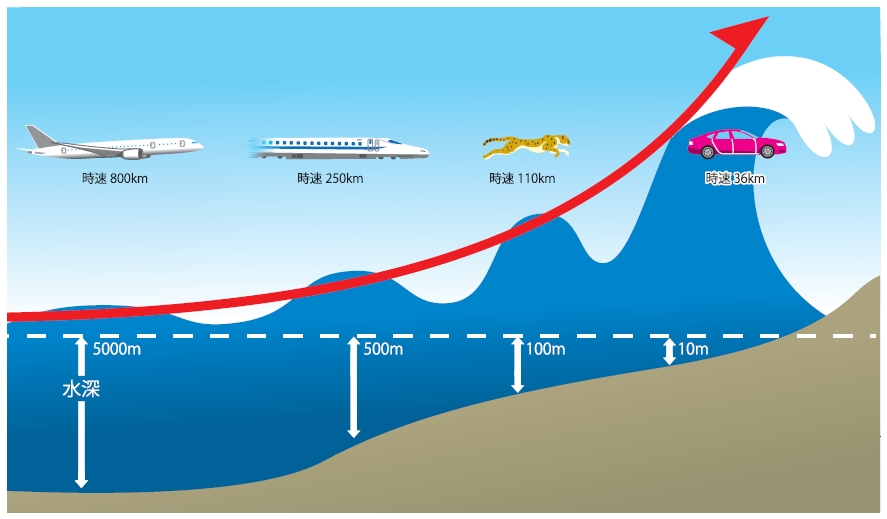
出展:気象庁リーフレット「津波防災」より
そしてこの性質があるからこそ、津波は海岸付近でその高さがどんどん高くなっていくんです。
先ほどの図にもありましたが、津波のスピードは海岸付近では遅いですよね?
(とはいっても、時速36kmと自動車なみのスピードです)
しかしそれより遠いところでは、相変わらずより速いスピードで波が動いているわけです。
そうなると、ある時点で後ろの津波が前に追いつきます。
結果として、前の波にエネルギーが集中して波高が高くなってしまうことになります。
本書ではこのことについて実に丁寧に描かれており、津波のメカニズムをよく理解することができると思います。
よく三陸地方などで見られるリアス海岸(私の学生時代ではリアス式海岸と学んでいましたが、最近はリアス海岸と呼んでいるようですね)では、津波の高さがさらに増幅されると言われていますが、その理由もこの長波によるものであることが分かります。
津波はとてつもない速さでやってきて、しかも壁のように押し寄せてきます。
そしてその壁はずっと、ずっとはるか遠くまで続いてすべてを飲み込んでしまうのです。
対策としてはできるだけ高台に逃げることしかありません。
私たちは、やはりこのことをしっかりと意識していかなければならないと思います。
まとめです
今回は防災を考えるための一冊として保坂直紀さんの「謎解き・津波と波浪の物理」を取り上げました。
波の現象、つまり波動現象については高度な数学が必要になります。したがってその内容も難しいものになりますが本書は数式をほぼ使わずに現象を丁寧にかみ砕いて説明されていると思いました。
そして本書は(科学の)ものごとの考え方においても非常に重要なアドバイスをされていると感じました。具体的には
- 複雑な現象を単純化して考えることでその本質を得る
- 現象を説明するのに一歩ずつ進むのも一つの方法
- もしくは結論の「見当」を付けてそれを導くために進めていく方法
といったことです。これは科学はもちろん、一般のどのような問題にも適用できる考え方だと思います。本の中でこのような考え方を波の現象に当てはめて解説もされていますので、そういった意味では科学的思考の実践書とも言えるのではないかと思います。
そして大事なことは、現象をつぶさに観察することなのでしょう。
波はどうして正面に押し寄せるのか?といった話題が本書にありましたが、これは読んでて確かにそうだとハッとしました。このことも長波の性質によるものなのですが、この理由についてはぜひ本書をご覧ください。大変明快な解説でした。
私の家は比較的海に近いので気分転換に訪れることも多いのですが、この事を知った後からじっくりと波を見つめるようになりました。
津波は日本の地理から考えて、今後も度々押し寄せてくることは間違いありません。
しかしその津波がどのようなものかを知り、対策することができれば被害を受けるリスクは減らせるはずです。
本書はその足掛かりとしてぜひお手に取っていただきたい一冊だと思います。



